Introduction to Linear programming with Python
From a brief overview to full implementation on a use case, lets try to understand the need, means and deeds of the classical approach.
Introduction
Linear programming is the technique used to maximize or minimize a function. The idea is to optimize a complex function by best representing them with linear relationships. In simpler terms, we try to optimize (to maximize or minimize) a function denoted in linear terms and bounded by linear constraints.
Use case— Miracle worker
Let’s try to formalize an use-case and carry it forward throughout the article. Suppose you are a magical healer and you goal is to heal anyone who asks for help. The more you are able to heal someone, the better. Your secret behind the healing is 2 medicines, each of which uses special herbs. To create one unit of medicine 1 , you need 3 units of herb A and 2 units of herb B. Similarly, to create one unit of medicine 2, you need 4 and 1 units of herb A and B respectively. Now medicine 1 can heal a person by 25 unit of health (whatever it is) and medicine 2 by 20 units. To complicate things further, you only have 25 and 10 units of herb A and B at your disposal. Now the question is, how many of each medicine will you create to maximize the health of the next person who walks in?
Modeling the problem
First let’s try to identify the objective (what we want to do and how) and constraint (the bounding functions) of the stated problem.
As it’s clear from the problem, we want to increase the health by as many units as possible. And medicines are the only thing which can help us with it. What we are unsure of, is the amount to each medicines to create. Going by a mathematician’s logic, lets say we create x units of medicine 1 and y units of medicine 2. Then the total health restored can be given by,
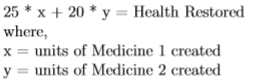This is the objective function, which we want to maximize. Now both the medicines are dependent on the herbs which we have in finite quantity. Let’s understand the constraints. If we create x and y units of medicine 1 and 2,
- We use 3 * x + 4 * y units of herb A. But we only have 25 units of it, hence the constraint is, our total usage of herb A should not exceed 25, denoted by,
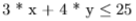* We use 2 * x + 1 * y units of herb B. We have 10 units of it, hence the constraint is, our total usage of herb B should not exceed 10, denoted by,
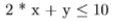* Also the amount of medicines created cannot be negative (doesn’t make sense) hence, they should be equal or greater than zero, denoted by,
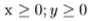#### Solution — Graphical representation
One way to solve the problem is by representing it into graph which requires plotting the functions, constraints and finding any point of interest. Let’s plot our functions and see what we can infer from it.
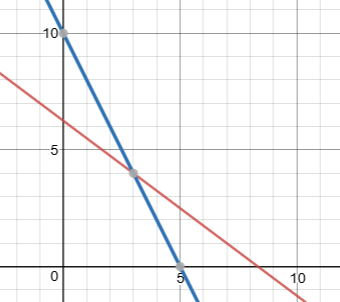Plotting constraint of herb A as Red and herb B as Blue line. Point of intersection is (3,4)The point of intersection, as obvious, from the plot is (3, 4), which says, If we create 3 units of medicine 1 and 4 units of medicine 2, considering the constraints on herbs, we are best equipped to heal the next patient. Intuitively, we wanted to find a solution which satisfy all of our constraints. As the constraint have few variables (only x and y ), transforming the problem into graph of lower dimension, we can visualize it as a 2D plot. With constraints on herbs being transformed into lines, our solution now transforms into a point of intersection. To make matter things better, it was on the positive quadrant, satisfying our 3rd constraint.
But what about problems with larger variable count? or with more constraints? wouldn’t it be difficult to plot and visualize them all? And do you always want to plot and solve these kinds of problems? Lets try to leverage modern computing prowess.
Solution — Python Programming
Python has a nice package named PuLP which can be used to solve optimization problems using Linear programming. To start with we have to model the functions as variables and call PuLP’s solver module to find optimum values. Here it goes,
Lets try to understand the code,
- Line 1–2: We import the PuLP package.
- Line 4–5: We define our problem by giving a suitable name, also specifying that our aim is to maximize the objective function.
- Line 7–9: Here, we define LpVariable to hold the variables of objective functions. The next arguments specifies the lower and upper bound of the defined variable. As per 3rd constraint, its non-negative, hence made second argument as 0 and 3rd as None (in-place of infinity). The last argument says if the required output is discrete or continuous.
- Line 11–12: Denotes the objective function in terms of defined variables, along with a short description.
- Line 13–15: Entering the herb’s constraints in terms of variables.
- Line 17–18: Output the objective and constraints into a file for portability and reuse. (Next time just load and run)
- Line 20–21: This calls the solver module and optimizes the functions. Now lets review the output,
As evident, the solution was optimum and similar to what we got from graphical representation.
Conclusion
Moving forward from this basic example, the true potential of optimization is showcased when we try to solve real world complex problems. Be it trying to find optimum distribution of funds to maximize country’s economy or trying to find best blend of materials to lower a building’s cost but maximize its life. As the problem gets complex, it makes sense to move from a manual to more say, efficient and automated, mode of solution hunting process. That’s when we can leverage python.
Find more such articles on my **personal site*.*
Cheers.