The Invariant principle — Introduction and examples
Understand the famous mathematical property which acted as bane for several complex real life problems and still kicks a punch here and there.
Introduction
The dictionary defines ‘invariant’ as ‘never changing’, and well that’s really all there is. Invariant in mathematics, is a property held by a mathematical object, which remains same even after repetitive transformation of the object. If for some objects that property is different, then we can never reach from the original object to the newer ones, by trying the same transformations. This may sound tricky, but its really helpful and in some cases may even solve the problem.
Types
There are basically two broad categories,
- Invariance: Property that stays constants.
- Mono-variance: Property that changes in only one-direction. Its either always increasing or decreasing. As Arthur Engel said it, “Invariance principle is a heuristic principle, its best learned by experience”, lets try to solve some examples to understand.
Example 1: Lone survivor
Statement: Suppose there are 1 to 1000 numbers written on a paper. At each step, we select any two numbers (randomly) and replace them with their difference. Is it possible to have 243 in the end as the only remaining number?
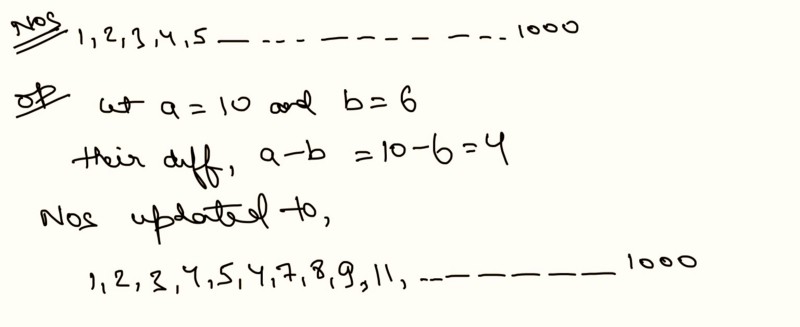Inference: Well that’s good question to start with, and may get tricky for some. The brute force logic says to start with all the numbers and keep trying all the possible combinations of selecting 2 numbers out of 1000. Then do it again, and again and if you ever reach 243 in the end, the answer is ‘yes’ otherwise, ‘maybe’ as there are still many ways left to solve this. Enter invariance. (Note, try to find some property which is never changing as we perform the operation before going further)
Solution:
#### Example 2: All equal
Statement: A circle is divided into 6 sectors, then the numbers 1, 0, 1, 0, 0, 0 are written into the sectors (clockwise). At each step, you increase two neighboring sector’s number by 1. Is it possible to have all sectors with same number after some steps?
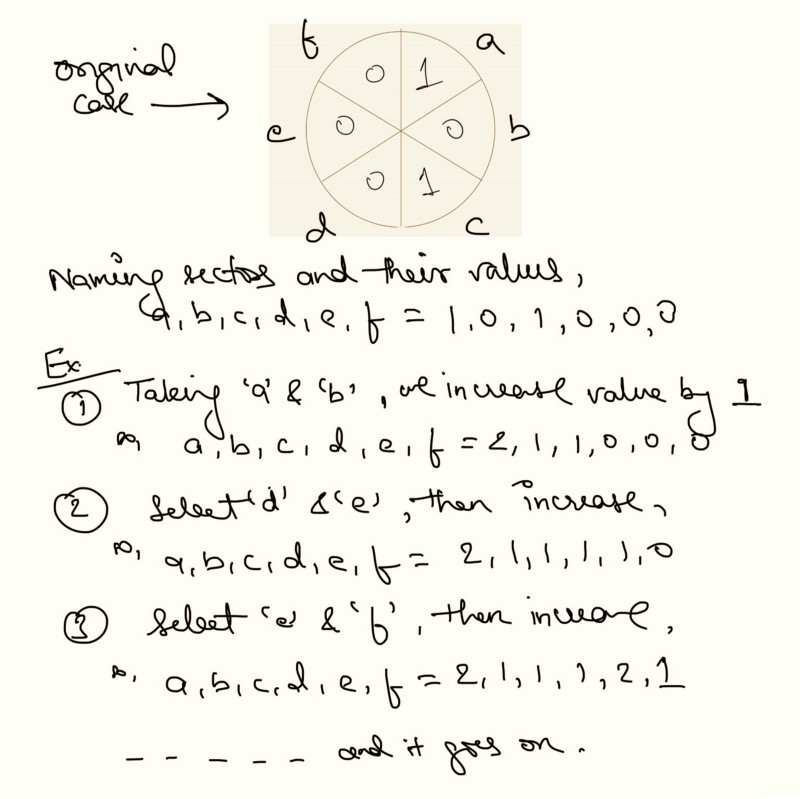**Inference: **Again, we have many possibilities of selection, and hence operation can be performed for any pair out of 6. Going one level down, again we select any pair out of 6. One difference from the previous question, this never terminates unless you have the solution i.e. all numbers are same. Hence, you may perform brute force for 1000s of levelscand solution state will still be a ‘maybe’.
Solution:
#### Example 3: Set for life!
**Statement: **Start with set {3, 4, 12}. In each step, choose any two numbers say a, b (randomly) and replace them with 0.6a — 0.8b and 0.8a + 0.6b. Is it possible to reach {4, 6, 12}?
**Inference: **Note the order doesn’t matter (set), all thats required is somehow by performing the operations can we transform the original set to the final one.
Solution:
### Conclusion
Simple knowledge of invariance and it’s application can lead to drastic reduction in solution space. As evident, we transformed the nearly impossible brute force solution to a single line. The main problem is to determine whether the problem has a invariance hidden beneath and then finally identifying it. Once done the solution quite within reach.