The art behind Fractals

by Mohit Mayank

Fractals !?

Recursion

Self-similarity

Fractal dimensions

A fractal is a never-ending pattern that repeats itself at different scales (either visually or statistically)

They are created by repeating a simple process over and over in an ongoing feedback loop.

They have their own geometry (fractal geometry) and could have non integer dimensions, like ~1.584 dimensions!

"Clouds are not spheres, mountains are not cones, coastlines are not circles and bark is not smooth, nor does lightning travel in a straight line." - Benoit Mandelbrot

What do we mean by fractal dimensions?

Aim of this talk

1. Explore ways of creating complex but beautiful fractals

 

2. Understand how trivial actions lead to non-trivial patterns

 

3. Discuss their applications and presence in nature

 

4. Fractals are part of a bigger animal - **revealed later** :)

 

"Fractals are a paradox. Amazingly simple, yet infinitely complex. New, but older than dirt."

ACT I: Chaos Game

a iterative random game with not so random outcome

Steps in Chaos Game

1. Choose some fixed points (vertices)  in a 2D space

 

2. Choose one dynamic point, we will move this a lot in the game (point)

 

3. By some logic, iteratively select one of the vertices (random, ..)

 

4. Move the point closer to the selected vertex by some proportion of their distances (compression ratio)

 

But how?

We understand by considering Sierpiński triangle

Creating a fractal is nothing but apply the same operations again and again....

f3(x, y) = (x/2 + 1/4, y/2+ 1/2)

These operations can be written as,

f1(x, y) = (x/2, y/2)
f2(x, y) = (x/2 + 1/2, y/2)

ACT II: Lindenmayer system

a string re-writing engine dev by a biologist

 
 

Steps in Lindenmayer system

1. Define unique characters (variables) and using them write down a string (axiom)

Ex: variable = {A,B}; axiom = "A"

 

2. Define some string replacement rules, which replaces one variable with another string (rules)

Ex: Two rules (A → AB), (B → A)

 

3. Iteratively perform string replacement and transform the string to patterns (by turtle rendering engine)

Ex: "A" --> "AB" --> "ABA" --> "ABAAB" --> ....

ACT III: Escape-time fractals

color the space by using a formula

Mandelbrot set

1. Define a complex 2D space, where x-axis showcase real numbers and y-axis showcase imaginary numbers

 

2. Pick one complex number (c) and pass its values iteratively into the formulae,                                  

 

3. Color the space w.r.t. logic: black - if c doesn't explode, else other color (color showcase how quickly 'c' explodes)

 
 
z_{n+1} = z_{n}^2 + c ; z=0

ACT IV: More fractals!!

in nature, if not then application and finally conclusion

Fractals in Nature

Fern similar to stem which inturn similar to frond

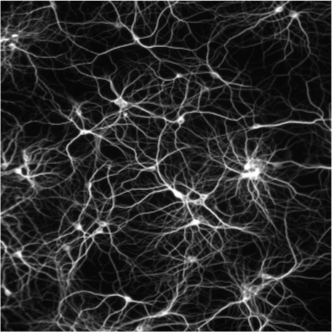
Neuron from human cortex

A hurricane is a self-organizing spiral in the atmosphere, driven by the evaporation and condensation of sea water.

mountains peaks (its computer generated)

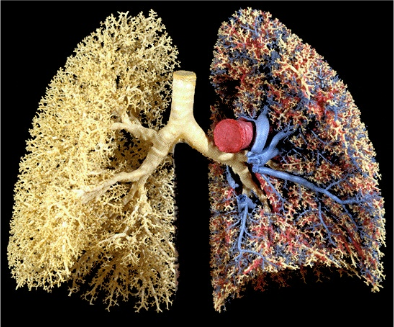
Fractals in Nature Part 2

Fractal river network in China

Our lungs are branching fractals

Biggest fractal ever - the spiral galaxy :)

Top view of Himalayan mountains

Koch snowflake

~1.25 dimensions!

 

In the 1990s Nathan Cohen became inspired by the Koch Snowflake to create a more compact radio antenna using nothing more than wire and a pair of pliers. (Left mouse click to see the effect)

Landscape

specially mountains are very much fractals

In 1978 Loren Carpenter wanted to make some computer-generated mountains. Using fractals that began with triangles, he created an amazingly realistic mountain range. (Press R to toggle state, A to toggle animation and left mouse click to change shape)

Hilbert curve

a type of space-filling curve, rendering till order 5

Ideal for transforming 2D grids into 1D domain because of its convergence property. Increases accuracy when used in CNN's input.

The Barnsley Fern

representation of black spleenwort fern

Generate a realistic fern with just some formulas !

Menger sponge

three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet

Today, antennae in cell phones are shaped as the Menger Sponge, the box fractal or space-filling fractals - as a way to maximize receptive power in a minimum amount of space (Move the mouse to rotate, mouse wheel to zoom and click to increase level)

Fractals are part of bigger picture - Chaos Theory !

 
  • Deterministic systems are unpredictable: take two starting states which are very, very similar to each other - over time the states will diverge and re-converge in unpredictable ways.
 
  • Oddly, the system is unpredictable but sometimes when observed over large period of time, it follows a pattern.
  • These patterns seems to revolve around a force called attractors, and as usually they are not in perfect smooth shape, they are called a strange attractor. This is what a fractal represents!
  • Ex: a healthy heart beats in a periodic (nonchaotic) pattern, and healthy brain waves are chaotic. Conversely, the dangerous fibrillation of a heart in trauma shows chaotic patterns, and the brainwaves seen during epileptic seizures are periodic.                       

"Tyrannosaurus doesn't obey a set pattern or park's schedule...the essence of chaos....a shorthand is the butterfly effect" -- Ian Malcolm (Jurassic Park - 1993)

Recap

 

1. We discussed the characteristics of fractals, especially the fractal dimension

 

2. We saw "Iterative function system" of drawing fractals - stochastic (chaos game) and deterministic (transformation)

 

3. We saw "L systems" - a string re-writing fractal maker (recursive)

 

4. We saw "Escape-time system" - uses formulae at each point in space

 

5. Saw additional fractals and their applications. Fractals in Nature.

 

6. Connected fractals to Chaos Theory.

Thank you

References

1. The Fractal foundation

2. Fractals and the Chaos Game

3. anuraghazra github

4. cassiofb-dev gitHub

5. HWS maths

6. Coding train landscape

7. TimSherbert

8. cbrwn

9. Mohit Mayank blog

Â